भूमितीतील अत्यंत महत्त्वाचे प्रमेय! इ.स.पूर्व सहाव्या शतकात ग्रीक गणिती पायथागोरस यांनी या प्रमेयाची तर्कशुद्ध सिद्धता दिली असे मानले जाते; पण या प्रमेयाची गणितज्ञांना इतकी भुरळ पडली की, आजपर्यंत या प्रमेयाच्या ३७०पेक्षा जास्त सिद्धता उपलब्ध आहेत, ज्यांचे एक स्वतंत्र पुस्तक आहे!
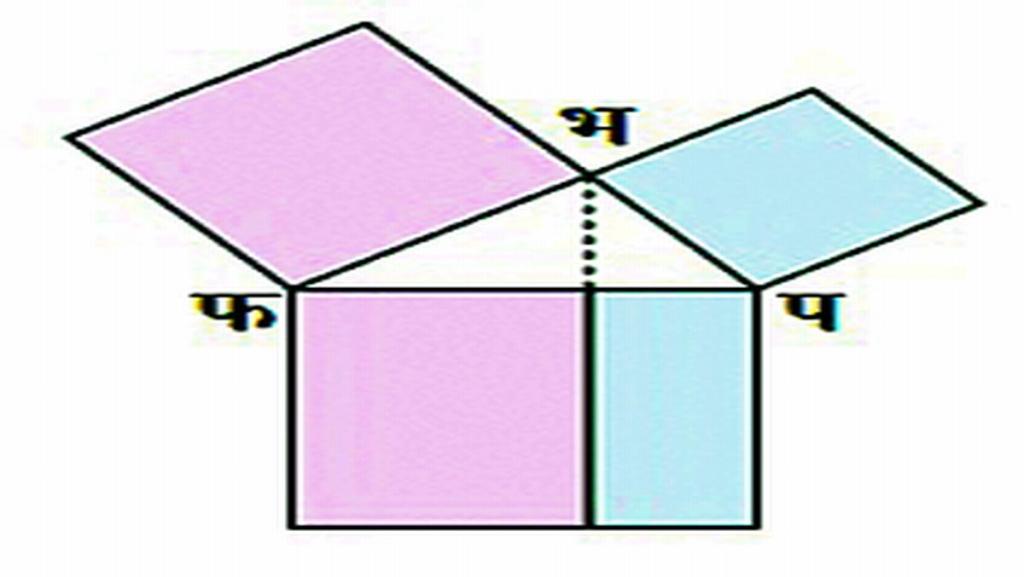
‘काटकोन त्रिकोणात कर्णाचा वर्ग इतर दोन बाजूंच्या वर्गांच्या बेरजेइतका असतो’ असे विधान असलेले हे प्रमेय शाळेत इयत्ता सातवी-आठवीतच ओळखीचे होते. त्रिकोणमिती तर संपूर्णपणे या प्रमेयाच्या आधारावरच उभी आहे. त्रिकोणमितीय गुणोत्तरे, नित्य समीकरणे, शाब्दिक उदाहरणे सोडवणे हे या प्रमेयाविना अशक्य आहे. प्रतलीय निर्देशक भूमितीत दोन बिंदूंमधील अंतर काढण्याचे सूत्र देणारे हे प्रमेय उच्च गणितातही त्रिमितीय भूमिती, सदिश राशी (व्हेक्टर्स), संगणकातील ‘बबल सॉर्ट’सारखी रीत (अल्गोरिदम) शिकताना साथसंगत करते. याशिवाय भौतिकशास्त्र, स्थापत्यशास्त्र, नौकानयनशास्त्र, भू-सर्वेक्षणशास्त्र आदींमध्ये पायथागोरसचे प्रमेय लागतेच.
काटकोन त्रिकोणाचा कर्ण ‘क’ आणि इतर दोन बाजू ‘अ’ व ‘ब’ घेतल्यास पायथागोरसचे प्रमेय अ२+ ब२= क२ या समीकरणात मांडता येते. हा गुणधर्म वैदिक काळी भारतात यज्ञवेदी बांधण्यासाठी तसेच इजिप्तमध्ये पिरॅमिड्स बांधण्यासाठी वापरल्याचे उल्लेख मिळतात. पायथागोरसपूर्वी सुमारे दोनशे वर्षांपूर्वी बौधायन शुल्बसूत्रात हे सूत्र वापरल्याचा पुरावा आहे. अ = ब = १ घेतल्यास क = न्न्२ अशी अपरिमेय संख्या मिळते; यावरून शुल्बसूत्रकारांनी न्न्३, न्न्५ अशा लांबीचे रेषाखंड काढण्यासाठी त्या सूत्राचा वापर केला होता. पायथागोरसच्या प्रमेयावरून आणखी अनेक महत्त्वाचे गुणधर्म मिळतात. उदाहरणार्थ, काटकोन त्रिकोणात कर्णावर काढलेल्या अर्धवर्तुळाचे क्षेत्रफळ इतर दोन बाजूंवर काढलेल्या अर्धवर्तुळांच्या क्षेत्रफळांच्या बेरजेइतके असते. कोणत्याही सुसम बहुभुजाकृतीसाठीही (रेग्युलर पॉलिगॉन) हा गुणधर्म सिद्ध करता येतो.
अ२ + ब२ = क२ या सूत्रात जर अ, ब, क या नैसर्गिक संख्या असतील, तर त्यांना पायथागोरसचे त्रिकूट म्हणतात. (३,४,५), (५,१२,१३) अशी पायथागोरसची त्रिकुटे मिळवण्यासाठी युक्लिडपासून अनेक गणितज्ञांनी विविध सूत्रे दिली आहेत. विविध स्पर्धा परीक्षांतही या त्रिकुटांवर आधारित प्रश्न विचारले जातात. (८८२०९, ९०२८८, १२६२२५) या पायथागोरसच्या त्रिकुटात काही विशेष आढळते का ते पाहा बरे!
गणितज्ञ केप्लर (इ.स. १५७१-१६३०)
यांनी ‘केप्लर त्रिकोण’ तयार करताना पायथागोरसचे प्रमेय आणि सुवर्णगुणोत्तर यांचा वापर केला. केप्लरच्या पुढील विधानात पायथागोरसच्या प्रमेयाचे भूमितीतील अढळ स्थान अधोरेखित होते : ‘भूमितीमध्ये दोनच मोठी रत्ने आहेत, एक म्हणजे पायथागोरसचा सिद्धान्त आणि दुसरे म्हणजे सुवर्ण गुणोत्तर!’
– शोभना नेने
मराठी विज्ञान परिषद,
संकेतस्थळ : http://www.mavipa.org
ईमेल : office@mavipamumbai.org