कुतूहल : लघुग्रहांची, धूमकेतूंची भ्रमंती

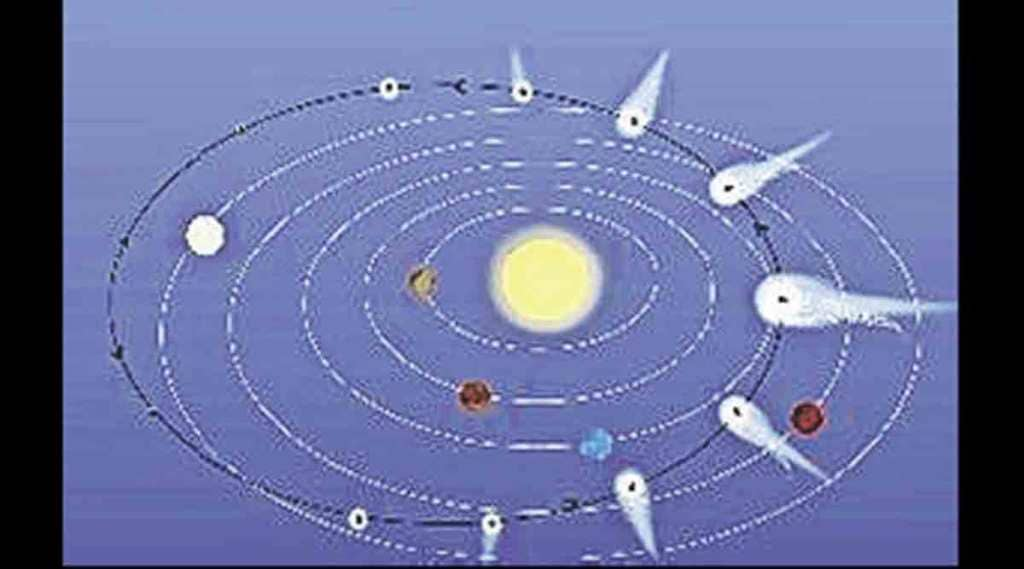
आपल्या ग्रहमालेतल्या अनेक नव्या लघुग्रहांचा आणि धूमकेतूंचा सतत शोध लागत असतो. या नुकत्याच शोधल्या गेलेल्या लघुग्रहांच्या वा धूमकेतूंच्या कक्षांची काहीच माहिती नसते. सुरुवातीच्या मोजक्या निरीक्षणांवरून या कक्षा नक्की कराव्या लागतात. एखाद्या ग्रहाच्या कक्षेवरून त्याचे स्थान शोधून काढण्याचे गणित हे काहीसे सरळ गणित आहे. परंतु काही मोजक्या निरीक्षणांवरून, एखाद्या नव्या लघुग्रहाची किंवा धूमकेतूची कक्षा ओळखणे, हे कठीण काम आहे. अशा प्रकारच्या गणितात क्रांती घडवून आणणारे गणितज्ञ म्हणजे जर्मनीचे कार्ल फ्रिडरिश गाऊस.इटालीच्या जिऊसेप्पे पिआत्सी यांनी १८०१ साली सिरीस या लघुग्रहाचा शोध लावला. शोधानंतर एका महिन्याने हा लघुग्रह सूर्याच्या तेजामुळे दिसेनासा झाला. नंतर काही काळाने तो दिसण्याची अपेक्षा असतानाही सापडला नाही. त्यासाठी, गाऊस यांनी एक नवी गणिती पद्धत वापरून, त्याद्वारे या लघुग्रहाच्या अपेक्षित स्थानाचा अंदाज वर्तवला. त्यांच्या गणितानुसार अल्पकाळातच हा लघुग्रह पुन्हा शोधला गेला. प्रथम गाऊस व त्यानंतर फ्रान्सच्या आंद्रे-मारी लेजांडर यांच्या प्रयत्नांतून या पद्धतीचा पुढे विकास झाला. ही पद्धत आता ‘लीस्ट स्क्वेअर मेथड’ या नावे ओळखली जाते. समजा एखादा चल घटक, अनेक अचल घटकांवर अवलंबून आहे. अशा चल घटकाचा अचल घटकांशी असलेला संबंध, गुणांकांच्या मदतीने गणिती सूत्रात मांडता येतो. त्यासाठी चल घटकांचे निरीक्षणांद्वारे मापन करून, या पद्धतीद्वारे ते गुणांक काढून, चल घटकाचा अचल घटकाशी असलेला संबंध दर्शवणारे गणिती सूत्र स्पष्ट करता येते. निरीक्षणांची संख्या जितकी अधिक, तितकी या पद्धतीतील अचूकता अधिक. ही पद्धत लघुग्रहांच्या किंवा धूमकेतूंच्या कक्षा नक्की करण्यासाठी अनेकदा वापरली जाते.